Tableau(태블로) 사용법 차트 그리기 : 박스 플롯(Box Plot)
Tableau(태블로)는 데이터 시각화에 좋은 도구입니다. 무료로 다운로드하여 14일 동안 경험해 볼 수 있습니다. 차트 그리기는 엑셀보다 쉽고, 빠르며, 직관적입니다. 오늘은 박스 플롯을 사례로 정리해 보겠습니다.
박스 플롯은 엑셀로 차트를 표현했던 분들에게는 생소할 수 있습니다. 그러나 박스 플롯은 정상 범위를 벗어나는 '아웃라이어'를 쉽게 찾을 수 있게 해 줍니다. 먼저 정규 분포도에 대해 간단히 살펴보아 쉽게 통계적 개념을 이해할 수 있도록 정리하겠습니다.
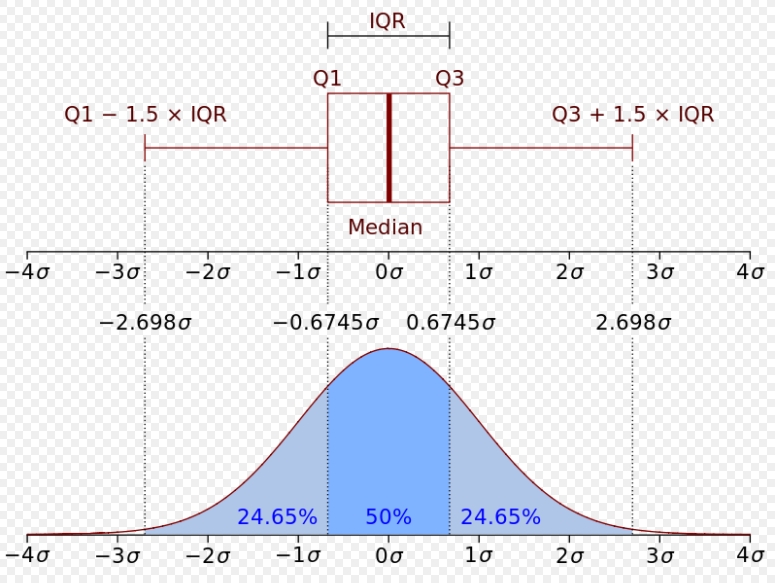
위 그림은 박스 플롯과 정규분포도와 비교함으로써 박스 플롯의 통계적 의미를 설명하였습니다.
기초 통계
1. 중앙 값(Median)
말 그대로 데이터 셋의 정중앙에 있는 값을 의미합니다. 그러면 이건 어떻게 구할 수 있을까요? 간단합니다. 데이터 개수가 n이라면 n에 1을 더한 후에 2를 나누면 됩니다. 예제를 통해서 알아보겠습니다.
- 데이터 수 9개 (홀수) : 1 1 2 4 3 5 8 8 9
- 데이터 수 10개(짝수) : 1 1 2 3 4 6 8 9 8 10
위의 예제에서 보면 총데이터가 홀수인 경우와 짝수인 경우를 나누어서 설명하겠습니다. 총데이터의 개수가 9개인 경우는 먼저 데이터 셋을 오름차순으로 정렬한 후 (n+1)/2를 계산합니다. 즉, (9+1)/2를 하면 5가 됩니다. 그러면 5번째 값을 오름차순으로 정리한 데이터에서 찾으면 그것이 바로 중앙값(median) 되는 것입니다. 즉 M=3 입니다.
총 데이터의 개수가 10개인 경우는 (10+1)/2 = 5.5가 되므로, 이때에는 5번째(4)와 6번째(6) 값을 찾은 후에 그것의 절반을 구하면 됩니다. 즉, (4+6)/2 = 5로 하여 M=5가 됩니다.
2. IQR(InterQuartile Range)
위 정규분포의 그림에서 데이터의 범위를 사분 범위로 먼저 구분한 후 중간에 50%의 데이터들이 흩어진 정도를 의미합니다. 그래서 Q3 - Q1으로 IQR은 구해질 수 있는데, 여기서 Q1은 데이터의 중앙값과 맨 아래의 값의 중앙값을 의미하고, Q3은 데이터의 중앙값과 맨 위의 값의 중앙값을 의미합니다.
3. 사분위 양 끝단
아래 끝단 값은 Q1-(1.5*IQR), 위 끝단 값은 Q3+(1.5*IQR)를 계산하여 사분위 양 끝단을 계산합니다.
4. 아웃라이어
사분위 양 끝단을 벗어나는 값들을 '아웃라이어'라고 부릅니다.
태블로 박스 플롯(Box Plot)
샘플 엑셀 시트를 다운로드하여 태블로에 연결해 보겠습니다. 태블로를 열고 다운로드한 엑셀자료를 불러옵니다.
박스 플롯 그리는 방법

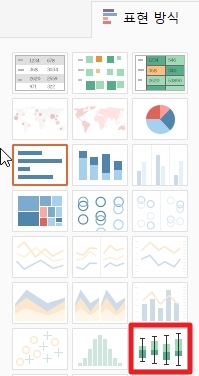
사이드바에서 '학생 번호'를 클릭한 후 Ctrl 키를 누른 채 '역사'를 선택합니다. 오른쪽 표현방식에서 차트 유형을 '박스 플롯'을 선택해 줍니다.
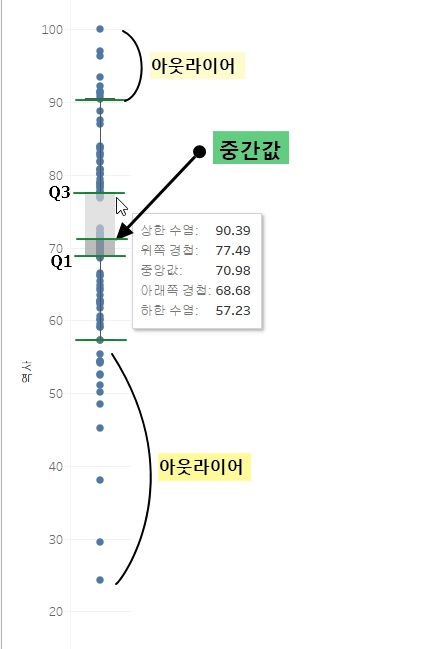
박스 플롯의 모양과 맨 위 정규 분포도와 함께 비교해서 보면 박스 플롯이 어떤 역할을 할 수 있는지 알 수 있습니다. 박스 플롯은 중간값(M)과 IQR(Q3-Q1)을 찾아주며 사분위 양 끝단을 벗어난 '아웃라이어' 데이터를 쉽게 찾아 주는 역할을 하게 됩니다.
이전에 작성했던 포스팅을 참조하시면 더 구체적 박스 플롯 사례를 살펴보실 수 있습니다.
'태블로(Tableau)' 카테고리의 다른 글
| 태블로(Tableau)에서 "특정 차원-테이블 계산" 가장 쉽게 이해하는 방법, 2개 기준만 알면 됩니다 (0) | 2021.09.02 |
|---|---|
| 태블로에서 시간 차이를 구하는 계산된 필드 만드는 방법 (0) | 2021.08.30 |
| Tableau(태블로) 사용법 차트 그리기 : 스캐터 플롯(Scatter Plot) (0) | 2021.04.18 |
| Tableau(태블로) 사용법: 엑셀 데이터 전처리, 태블로 프렙으로 한다. (0) | 2021.04.10 |
| Tableau(태블로) 사용법 차트 그리기 : 파이 차트(Pie chart) (0) | 2021.04.08 |





